Método Scheiner
Poner en estación una montura ecuatorial por el método Scheiner

¡La estrella no se mantiene en el centro del ocular!
Imagina que tienes una montura ecuatorial motorizada, apuntas a una estrella que se encuentre en cualquier punto del cielo, la centras en un ocular y la observas durante un tiempo; si estás así durante unos minutos, verás que la estrella no se mantiene en el centro del ocular, sino que se va alejando constantemente del centro haciendo una especie de baile de vaivén alrededor de la dirección de «huida».
Estos «extraños» movimientos se deben a varias razones, principalmente:
● Las limitaciones del motor que mueve el eje de ascensiones rectas (o mejor dicho, del sistema de ruedas dentadas y bisinfines que forman parte del mecanismo que hace rotar el eje de ascensiones rectas al mismo ritmo que el movimiento de rotación terrestre) estas limitaciones hacen que unas veces este eje rote ligeramente más rápido que la propia Tierra (con lo que la estrella se «retrasa» en el ocular) y otras veces más lento (con lo que la estrella se «adelanta»). A este efecto se le denomina «error periódico» y todas las monturas lo sufren en mayor o en menor medida.
● El eje de ascensiones rectas no está perfectamente apuntando al polo norte celeste. Este error de «puesta en estación«, puede analizarse como dos errores independientes en los ejes de altura y azimut (horizonte).
● El mal equilibrado/contrapesado del conjunto puede afectar a aumentar las derivas tanto en declinación como en ascensión recta
A su vez, si representamos en el ocular el sistema de coordenadas ecuatorial (Ascensión Recta/Declinación), es decir si disponemos de un ocular reticulado y orientamos sus ejes con los ejes ecuatoriales, podemos representar las derivas de la estrella (separación del centro por unidad de tiempo) como la suma de dos derivas independientes una en ascensiones rectas (AR) y otra en declinaciones (Dec).
El método de Scheiner: un poco de matemáticas
El sistema de ecuaciones que expresan las derivas en declinación y en ascensión recta (expresadas por comodidad como en unidades h de ángulo horario) de una estrella viene dado por:
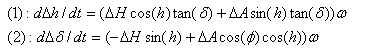
, donde

Estas ecuaciones se deducen a partir de diferenciar las ecuaciones que expresan el error en ángulo horario y en declinaciones, en base a un error en Azimut y Altura:
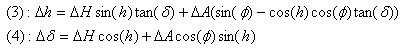
¡Divide y vencerás!
Las ecuaciones (1) y (2) vienen en nuestra ayuda si consideramos dos situaciones determinadas, en las que corregiremos los ejes de Altura y de Azimut de manera independiente.
Corrección en Azimut:
Imagina que apuntamos a una estrella en el meridiano:

El ángulo horario de una estrella que esté en cualquier parte del meridiano (no hace falta que esté en el ecuador o cerca de él) es de 0h, con lo que cos(h) = 1 y sin(h) = 0 y el sistema de ecuaciones (1) y (2) se convierten en:
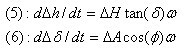
, es decir, que si medimos las derivas en declinación en unidades de desplazamiento por minuto, conoceremos el error de Azimut en esas mismas unidades de desplazamiento. Despejando los errores en Altura y Azimut en el sistema de ecuaciones (5) y (6) tenemos:
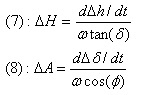
El problema es que en la práctica es difícil utilizar las medidas de la ecuación (7), pues tendríamos que excluir de las medidas de derivas en ascensiones rectas, los efectos del error periódico. Esto es aún posible si realizamos un ajuste lineal por mínimos cuadrados a los valores de derivas en AR: de la tendencia indicada por la recta resultante obtenemos las derivas puras en el eje.
Pero si nos atenemos al método clásico, habremos medido el error en Azimut y podremos corregirlo de manera precisa haciendo uso de la ecuación (8). Con un ordenador que realice tanto las medidas de derivas como los cálculos correspondientes, esto resulta bastante sencillo.
¿Has llegado hasta aquí? ¡Felicidades! Tienes el eje horizontal alineado con el polo.
¿Y el eje de Altura?
Ahora propongamos otra situación: apuntemos a una estrella que se encuentre en un ángulo horario de 6h:
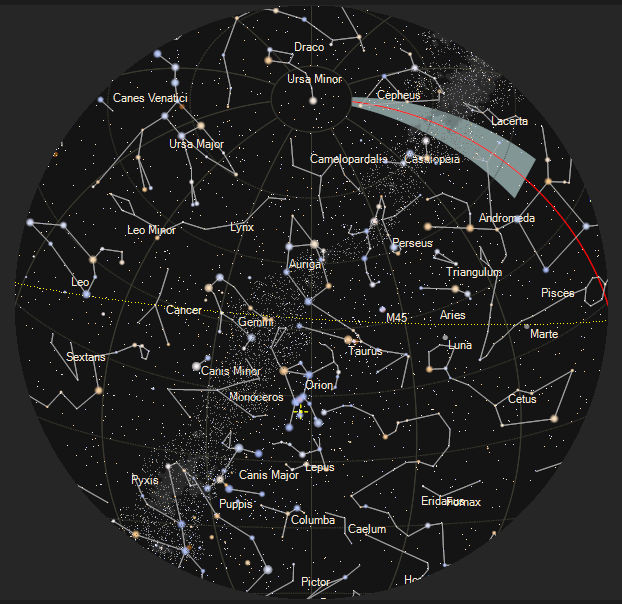
, o de 18h:
En ambas situaciones, resulta que cos(h) = 0 y sin(h) = ±1 y , con lo que el sistema de ecuaciones (1) (2) quedan de la siguiente forma:
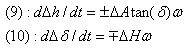
, o lo que es lo mismo:
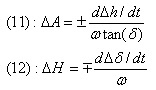
Siguiendo el mismo razonamiento que en el punto anterior, con la ecuación (12) resolvemos el error del eje de Altura, conocidas las derivas en declinaciones.
¿Ya está? ¿Está perfectamente alineada mi montura?
No. Vaya, idealmente sí, pero en la práctica no. ¿Por qué? Pues porque en la práctica no encontraremos dos estrellas que estén respectivamente a 6h/18h y a 0h en ángulo horario, y habremos elegido dos estrellas que aproximadamente están en esos ángulos.
Esas aproximaciones hacen que los términos cos(h) y sin(h) no sean exactamente 0 ó 1, sino, digamos 0.1 ó 0.98, por ejemplo. Esas pequeñas contribuciones del error del otro eje aumentan cuanto mayor es el error del otro eje y se hacen despreciables si el error del otro eje es pequeño o nulo.
Pero conociendo esas limitaciones podemos proceder de la siguiente manera:
1) Procedemos a corregir el eje de azimut. Como se ha visto en la deriva hay una contribución del error en el eje de altura, pero es mínima frente a la de azimut. A pesar de ello, se habrá corregido la mayor parte del error de azimut y este será muy pequeño.
2) Corregimos el eje de altura. El error de azimut, aún siendo mucho menor, todavía contribuye a las derivas, pero la mayor parte es debida al eje de altura.
3) Volvemos a corregir el error de azimut. El error en altura es tan pequeño ahora que su contribución a las derivas es despreciable. El eje de azimut queda corregido con suficiente exactitud.
4) Lo mismo con el eje de altura. Esta vez la contribución del error de azimut es nulo o despreciable y el eje de altura queda corregido con suficiente exactitud.
Por supuesto, podemos continuar afinando, pero también queremos sacar alguna foto ¿no?.
¿Y qué ocurre si elijo una estrella en el este y cerca del ecuador celeste para corregir el eje de Altura?
Pues no es del todo correcto, como veremos a continuación, pero en algunos casos puede ser que funcione. Veamos por qué.
Supongamos que medimos una estrella que esté en el ecuador (declinación = 0) en el este y a una altura de 15 grados, por ejemplo, es decir con ángulo horario de 19h aproximadamente:
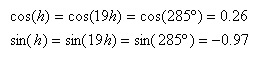
Como se puede observar, la contribución relativa de cada término no es nada despreciable y si sustituimos en la ecuación (2) encontraremos que las derivas anotadas se debe tanto al error de un eje como de otro de manera significativa. Este efecto se reduce cuanto mayor sea la latitud geográfica, pues el término cos(fi) (latitud) en (2) también disminuye.
Ahora bien, supongamos que hemos corregido previamente el eje de Azimut midiendo las derivas de una estrella en el meridiano. En este caso, el término:
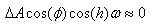
, puesto que el error en azimut es despreciable, sustituyendo en (2), tenemos que:
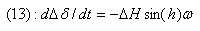
, es decir:
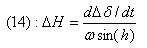
Es decir, podemos deducir el error en Altura con una estrella que esté en el este y en el ecuador (o en cualquier otra parte del cielo), siempre que previamente hayamos corregido el error en Azimut.
¿He de tener algo más en cuenta?
¡Sí!:
● Nivela bien la montura; si no, al corregir el eje de altura (o de azimut) ¡también estarás corrigiendo una pequeña cantidad del otro eje!
● Contrapesa bien el conjunto, si no las derivas que mides bien puden deberse en parte a la ¡fuerza de gravedad!
Y ¿Quién ideó todo esto?
Para conocer un poco más sobre el método Scheiner:
● «El método Scheiner» (español).
● «Polachsenjustierung» (alemán).
